Loops and iteration

library(tidyverse)

Learning goals

After this lesson, you should be able to:

Use the across() function
- Compare across() to an approach with pivot_longer() and pivot_wider()
Write a for loop in R to handle repeated tasks
Use the map() family of functions in the purrr package to handle repeated tasks

You can download a template Quarto file to start from here. Save this template within the following directory structure:

your_course_folder
- iteration
  - code
    - 09-iteration.qmd

Iteration across data frame columns with `across()`

Often we will have to perform the same data wrangling on many variables (e.g., rounding numbers)

diamonds %>%
    mutate(
        carat = round(carat, 1),
        x = round(x, 1),
        y = round(y, 1),
        z = round(z, 1)
    )

# A tibble: 53,940 × 10
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1   0.2 Ideal     E     SI2      61.5    55   326   4     4     2.4
 2   0.2 Premium   E     SI1      59.8    61   326   3.9   3.8   2.3
 3   0.2 Good      E     VS1      56.9    65   327   4     4.1   2.3
 4   0.3 Premium   I     VS2      62.4    58   334   4.2   4.2   2.6
 5   0.3 Good      J     SI2      63.3    58   335   4.3   4.3   2.8
 6   0.2 Very Good J     VVS2     62.8    57   336   3.9   4     2.5
 7   0.2 Very Good I     VVS1     62.3    57   336   4     4     2.5
 8   0.3 Very Good H     SI1      61.9    55   337   4.1   4.1   2.5
 9   0.2 Fair      E     VS2      65.1    61   337   3.9   3.8   2.5
10   0.2 Very Good H     VS1      59.4    61   338   4     4     2.4
# ℹ 53,930 more rows

dplyr provides the across() function for performing these repeated function calls:

# Option 1: Create our own named function
round_to_one <- function(x) {
    round(x, digits = 1)
}
diamonds %>% 
    mutate(across(.cols = c(carat, x, y, z), .fns = round_to_one))

# A tibble: 53,940 × 10
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1   0.2 Ideal     E     SI2      61.5    55   326   4     4     2.4
 2   0.2 Premium   E     SI1      59.8    61   326   3.9   3.8   2.3
 3   0.2 Good      E     VS1      56.9    65   327   4     4.1   2.3
 4   0.3 Premium   I     VS2      62.4    58   334   4.2   4.2   2.6
 5   0.3 Good      J     SI2      63.3    58   335   4.3   4.3   2.8
 6   0.2 Very Good J     VVS2     62.8    57   336   3.9   4     2.5
 7   0.2 Very Good I     VVS1     62.3    57   336   4     4     2.5
 8   0.3 Very Good H     SI1      61.9    55   337   4.1   4.1   2.5
 9   0.2 Fair      E     VS2      65.1    61   337   3.9   3.8   2.5
10   0.2 Very Good H     VS1      59.4    61   338   4     4     2.4
# ℹ 53,930 more rows

# Option 2: Use an "anonymous" or "lambda" function that isn't named
diamonds %>% 
    mutate(across(.cols = c(carat, x, y, z), .fns = function(x) {round(x, digits = 1)} ))

# A tibble: 53,940 × 10
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1   0.2 Ideal     E     SI2      61.5    55   326   4     4     2.4
 2   0.2 Premium   E     SI1      59.8    61   326   3.9   3.8   2.3
 3   0.2 Good      E     VS1      56.9    65   327   4     4.1   2.3
 4   0.3 Premium   I     VS2      62.4    58   334   4.2   4.2   2.6
 5   0.3 Good      J     SI2      63.3    58   335   4.3   4.3   2.8
 6   0.2 Very Good J     VVS2     62.8    57   336   3.9   4     2.5
 7   0.2 Very Good I     VVS1     62.3    57   336   4     4     2.5
 8   0.3 Very Good H     SI1      61.9    55   337   4.1   4.1   2.5
 9   0.2 Fair      E     VS2      65.1    61   337   3.9   3.8   2.5
10   0.2 Very Good H     VS1      59.4    61   338   4     4     2.4
# ℹ 53,930 more rows

When we look at the documentation for across(), we see that the .cols argument specifies which variables we want to transform, and it has a <tidy-select> tag. This means that the syntax we use for .cols follows certain rules. Let’s click this link to explore the possibilities for selecting variables.

Read through the “Overview of selection features” section to get an overall sense of the many ways to select variables.
Navigate back to the across() documentation and read through the Examples section at the bottom. Click the “Run examples” link to view the output for all of the examples.

Exercise: Using the diamonds dataset:

Transform the x, y, and z columns so that the units of millimeters are displayed (e.g., “4.0 mm”).
Convert all numeric columns into character columns.
- Hint: type is. and hit Tab in the Console. Scroll through the function options. Do the same with as.

Pick one of the two tasks above–how could you do this with a pivot_longer() and then a pivot_wider()?

What if we wanted to perform multiple transformations on each of many variables?

Within the different values of diamond cut, let’s summarize the mean, median, and standard deviation of the numeric variables. When we look at the .fns argument in the across() documentation, we see that we can provide a list of functions:

diamonds %>%
    group_by(cut) %>% 
    summarize(across(.cols = where(is.numeric), .fns = list(mean = mean, med = median, sd = sd)))

# A tibble: 5 × 22
  cut     carat_mean carat_med carat_sd depth_mean depth_med depth_sd table_mean
  <ord>        <dbl>     <dbl>    <dbl>      <dbl>     <dbl>    <dbl>      <dbl>
1 Fair         1.05       1       0.516       64.0      65      3.64        59.1
2 Good         0.849      0.82    0.454       62.4      63.4    2.17        58.7
3 Very G…      0.806      0.71    0.459       61.8      62.1    1.38        58.0
4 Premium      0.892      0.86    0.515       61.3      61.4    1.16        58.7
5 Ideal        0.703      0.54    0.433       61.7      61.8    0.719       56.0
# ℹ 14 more variables: table_med <dbl>, table_sd <dbl>, price_mean <dbl>,
#   price_med <dbl>, price_sd <dbl>, x_mean <dbl>, x_med <dbl>, x_sd <dbl>,
#   y_mean <dbl>, y_med <dbl>, y_sd <dbl>, z_mean <dbl>, z_med <dbl>,
#   z_sd <dbl>

What does the list of functions look like? What is the structure of this list object?

list_of_fcts <- list(mean = mean, med = median, sd = sd)
list_of_fcts

$mean
function (x, ...) 
UseMethod("mean")
<bytecode: 0x1392f3458>
<environment: namespace:base>

$med
function (x, na.rm = FALSE, ...) 
UseMethod("median")
<bytecode: 0x1595286a8>
<environment: namespace:stats>

$sd
function (x, na.rm = FALSE) 
sqrt(var(if (is.vector(x) || is.factor(x)) x else as.double(x), 
    na.rm = na.rm))
<bytecode: 0x109aaaf28>
<environment: namespace:stats>

str(list_of_fcts)

List of 3
 $ mean:function (x, ...)  
 $ med :function (x, na.rm = FALSE, ...)  
 $ sd  :function (x, na.rm = FALSE)

We’ll be working more with lists in upcoming lessons.

Case study: performing many different versions of an analysis

My number 1 use case for writing functions and iteration/looping is to perform some exploration or modeling repeatedly for different “tweaked” versions. For example, our broad goal might be to fit a linear regression model to our data. However, there are often multiple choices that we have to make in practice:

Keep missing values or fill them in (imputation)? (We’ll talk about missing data and imputation after Fall Break.)
Fit the model only on a certain group of cases?
Filter out outliers in one or more variables?
Transform certain variables? (e.g., log transformation)

We can map these choices to arguments in a custom model-fitting function:

impute: TRUE or FALSE
filter_to: This could be a set of string descriptions: “All cases”, “Group 1”, “Groups 1 and 2”
remove_outliers: TRUE or FALSE
outlier_sd_thresh: Cases that are more than this number of SDs away from the mean will be considered outliers and excluded

The tidyr package has a useful function called crossing() that is useful for generating argument combinations. For each argument, we specify all possible values for that argument. crossing() generates all combinations.

df_arg_combos <- crossing(
    impute = c(TRUE, FALSE),
    filter_to = c("All cases", "Group 1", "Groups 1 and 2"),
    remove_outliers = c(TRUE, FALSE)
)
df_arg_combos

# A tibble: 12 × 3
   impute filter_to      remove_outliers
   <lgl>  <chr>          <lgl>          
 1 FALSE  All cases      FALSE          
 2 FALSE  All cases      TRUE           
 3 FALSE  Group 1        FALSE          
 4 FALSE  Group 1        TRUE           
 5 FALSE  Groups 1 and 2 FALSE          
 6 FALSE  Groups 1 and 2 TRUE           
 7 TRUE   All cases      FALSE          
 8 TRUE   All cases      TRUE           
 9 TRUE   Group 1        FALSE          
10 TRUE   Group 1        TRUE           
11 TRUE   Groups 1 and 2 FALSE          
12 TRUE   Groups 1 and 2 TRUE

A function that implements the analysis and allows for variation in these choices:

fit_model <- function(df, impute, filter_to, remove_outliers) {
    if (impute) {
        df <- some_imputation_function(df)
    }
    
    if (filter_to=="Group 1") {
        df <- df %>% 
            filter(group==1)
    } else if (filter_to=="Groups 1 and 2") {
        df <- df %>% 
            filter(group %in% c(1,2))
    }
    
    if (remove_outliers) {
        df <- function_for_removing_outliers(df)
    }
    
    lm(y ~ x1 + x2, data = df)
}

But how can we iterate the fit_model() function over the combinations in df_arg_combos? We have two good options in R:

for loops
The purrr package (in the tidyverse) (general purpose functions for iterating other functions)

`for` loops

for (i in 1:10) {
    print(i)
}

[1] 1
[1] 2
[1] 3
[1] 4
[1] 5
[1] 6
[1] 7
[1] 8
[1] 9
[1] 10

The following for loops all have the same behavior.

We don’t have to use a numerical indexing variable to iterate:

groups <- c("group1", "group2", "group3")
for (g in groups) {
    print(g)
}

[1] "group1"
[1] "group2"
[1] "group3"

The single square brackets [i] get the ith element of a vector.

for (i in 1:3) {
    print(groups[i])
}

[1] "group1"
[1] "group2"
[1] "group3"

The seq_along() function generates an integer sequence from 1 to the length of the vector supplied. A nice feature of seq_along() is that it generates an empty iteration vector if the vector you’re iterating over itself has length 0.

seq_along(groups)

[1] 1 2 3

no_groups <- c()
seq_along(no_groups)

integer(0)

for (i in seq_along(groups)) {
    print(groups[i])
}

[1] "group1"
[1] "group2"
[1] "group3"

Often we’ll want to store output created during a for loop. Let’s see how we can fit linear regression models to subsets of data and store the results.

data(diamonds)

# Fit models of price vs. carat separately for each value of cut
unique_cuts <- diamonds %>% pull(cut) %>% levels()
lin_mod_results <- vector(mode = "list", length = length(unique_cuts))

for (i in seq_along(unique_cuts)) {
    this_cut <- unique_cuts[i]
    diamonds_sub <- diamonds %>%
        filter(cut==this_cut)
    # The double square brackets [[i]] accesses the ith element of a list
    lin_mod_results[[i]] <- lm(price ~ carat, data = diamonds_sub)
}

`purrr`

The purrr package contains general purpose functions for iteration. Let’s take a look the function reference.

The map() family of functions applies a given function (f in the image below) to each of the elements of a vector or list. A data frame is a special type of list. (We’ll talk more about lists later.)

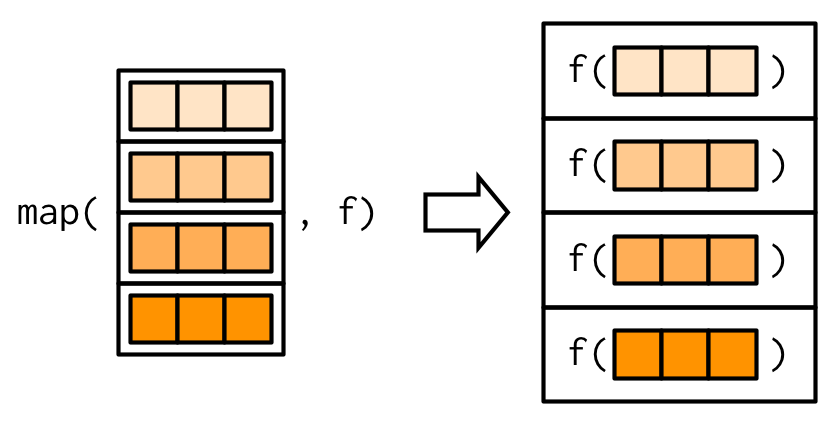
map() returns a list
map_chr() returns a character vector
map_lgl() returns a logical vector
map_int() returns an integer vector
map_dbl() returns a numeric vector
map_vec() returns a vector of a different (non-atomic) type (like dates)

The examples below show how map() iterates over each variable of a data frame to apply a function to that variable. In the picture above, we can view each of the horizontal rectangles as a variable in a data frame.

# Because map_chr expects the supplied function to give a single string, we get an error
# because the 3 factors (cut, color, and clarity) have both the "factor" and "ordered" class
map_chr(diamonds, class)

Error in `map_chr()`:
ℹ In index: 2.
ℹ With name: cut.
Caused by error:
! Result must be length 1, not 2.

# But map() has no such expectations
map(diamonds, class)

$carat
[1] "numeric"

$cut
[1] "ordered" "factor" 

$color
[1] "ordered" "factor" 

$clarity
[1] "ordered" "factor" 

$depth
[1] "numeric"

$table
[1] "numeric"

$price
[1] "integer"

$x
[1] "numeric"

$y
[1] "numeric"

$z
[1] "numeric"

map(diamonds %>% select(where(is.numeric)), mean)

$carat
[1] 0.7979397

$depth
[1] 61.7494

$table
[1] 57.45718

$price
[1] 3932.8

$x
[1] 5.731157

$y
[1] 5.734526

$z
[1] 3.538734

map_int(diamonds %>% select(where(is.numeric)), mean) # map_int gives an error because the result of mean() is a double (not an integer)

Error in `map_int()`:
ℹ In index: 1.
ℹ With name: carat.
Caused by error:
! Can't coerce from a number to an integer vector.

map_dbl(diamonds %>% select(where(is.numeric)), mean)

       carat        depth        table        price            x            y 
   0.7979397   61.7494049   57.4571839 3932.7997219    5.7311572    5.7345260 
           z 
   3.5387338

map(diamonds %>% select(!where(is.numeric)), n_distinct)

$cut
[1] 5

$color
[1] 7

$clarity
[1] 8

map_int(diamonds %>% select(!where(is.numeric)), n_distinct)

    cut   color clarity 
      5       7       8

purrr also offers the pmap() family of functions that take multiple inputs and loops over them simultaneously:

df <- tibble(
    string = c("apple", "banana", "cherry"),
    pattern = c("p", "n", "h"),
    replacement = c("P", "N", "H")
)

pmap(df, str_replace_all)

[[1]]
[1] "aPPle"

[[2]]
[1] "baNaNa"

[[3]]
[1] "cHerry"

pmap_chr(df, str_replace_all)

[1] "aPPle"  "baNaNa" "cHerry"

Exercise: Create your own small examples that show how pmap works with str_remove() and str_sub.

Application exercise

Reminder to reflect

As you work through this application exercise, make note: what is challenging? What feels comfortable? What insights do you gain from collaborating with others? What ideas/strategies do you want to remember going forward?

Goal: In the diamonds dataset, we want to understand the relationship between price and size (carat). We want to explore variation along two choices:

The variables included in the model. We’ll explore 3 sets of variables:
- No further variables (just price and carat)
- Adjusting for cut
- Adjusting for cut and clarity
- Adjusting for cut, clarity, and color
Whether or not to remove outliers in the carat variable. We’ll define outliers as cases whose carat is over 3 SDs away from the mean.

Exercise 1: Use crossing() to create the data frame of argument combinations for our analyses. Note that you can create a list of formula objects in R with c(y ~ x1, y ~ x1 + x2).

Solution

df_arg_combos <- crossing(
    mod_formula = c(price ~ carat, price ~ carat + cut,  price ~ carat + cut + clarity,  price ~ carat + cut + clarity + color),
    remove_outliers = c(TRUE, FALSE)
)
df_arg_combos

# A tibble: 8 × 2
  mod_formula remove_outliers
  <list>      <lgl>          
1 <formula>   FALSE          
2 <formula>   TRUE           
3 <formula>   FALSE          
4 <formula>   TRUE           
5 <formula>   FALSE          
6 <formula>   TRUE           
7 <formula>   FALSE          
8 <formula>   TRUE

Exercise 2: Write a function that removes outliers in a dataset. The user should be able to supply the dataset, the variable to remove outliers in, and a threshold on the number of SDs away from the mean used to define outliers.

Solution

remove_outliers <- function(df, what_var, sd_thresh) {
    df %>% 
        mutate(zscore = ({{ what_var }} - mean({{ what_var}}, na.rm = TRUE))/sd({{ what_var }}, na.rm = TRUE)) %>%
        filter(zscore <= sd_thresh)
}

Exercise 3: Write a function that implements the analysis versions specifically for the diamonds dataset. The user will not specify the dataset as an argument but will input the model formula and whether or not to remove outliers (cases whose carat is over 3 SDs away from the mean).

Solution

fit_model <- function(mod_formula, remove_outliers) {
    if (remove_outliers) {
        diamonds_clean <- remove_outliers(diamonds, what_var = carat, sd_thresh = 3)
    } else {
        diamonds_clean <- diamonds
    }
    
    lm(mod_formula, data = diamonds_clean)
}

Exercise 4: Write a for loop that stores the fitted linear models from all versions of the analysis.

Note that you can pull out the contents of a single data frame column in many ways. For a data frame df with a variable named x:

df$x
df %>% pull(x)
df[["x"]]

Solution

lin_mod_res_for <- vector(mode = "list", length = nrow(df_arg_combos))

for (i in seq_along(lin_mod_res_for)) {
    this_formula <- df_arg_combos$mod_formula[[i]] # Double [[ for the **list** of formulas
    this_remove_outliers <- df_arg_combos$remove_outliers[i] # Single [ for the **atomic vector** of logicals
    lin_mod_res_for[[i]] <- fit_model(
        mod_formula = this_formula,
        remove_outliers = this_remove_outliers
    )
}

Exercise 5: Use pmap() from purrr to replicate what you did with the for loop.

Solution

lin_mod_res_pmap <- pmap(df_arg_combos, fit_model)

Learning goals

Iteration across data frame columns with across()

Case study: performing many different versions of an analysis

for loops

purrr

Application exercise

Iteration across data frame columns with `across()`

`for` loops

`purrr`