Topic 3 d-separation (Part 1)
Learning Goals
- Review concepts of simulating DAGs in R
- Understand d-separation as a general means of identifying independence/dependence in arbitrarily complex causal diagrams
- Apply d-separation ideas to a case study: the birth weight paradox
Discussion: d-separation
A path \(p\) is blocked by a set of nodes \(Z\) (which could be the empty set) if and only if at least one of the two conditions below are met. (\(Z\) is the set of variables being conditioned on.)
- \(p\) contains a chain of nodes \(A \rightarrow B \rightarrow C\) or a fork \(A \leftarrow B \rightarrow C\) such that the middle node \(B\) is in \(Z\).
- \(p\) contains a collider \(A \rightarrow B \leftarrow C\) such that the collision node B is not in \(Z\), and no descendant of \(B\) is in \(Z\).
If \(Z\) blocks every path between two nodes \(X\) and \(Y\), then \(X\) and \(Y\) are d-separated, conditional on \(Z\), and are thus independent conditional on \(Z\).
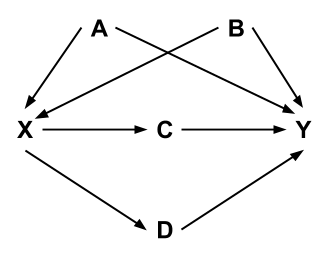
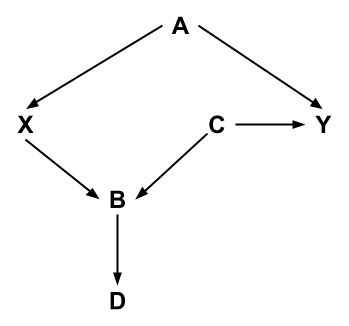
Discussion: The Birth Weight Paradox
To facilitate our discussion, key pieces of information and terminology from the article are summarized below.
Crude mortality rate ratio
\[\frac{\hbox{Infant mortality rate for maternal smokers}}{\hbox{Infant mortality rate for maternal non-smokers}} = 1.55\]
Adjusted mortality rate ratio: same ratio but arising from a logistic regression model in which birth weight was held constant. This was 1.09.
Stratum-specific mortality rate ratios
In low birth weight infants:
\[\frac{\hbox{Infant mortality rate for maternal smokers}}{\hbox{Infant mortality rate for maternal non-smokers}} = 0.79\]
In normal birth weight infants:
\[\frac{\hbox{Infant mortality rate for maternal smokers}}{\hbox{Infant mortality rate for maternal non-smokers}} = 1.80\]
In your groups, discuss the following questions. Make sure to take good notes because the first post in your Portfolio will be a careful analysis of this paper.
Throughout, remember that looking only at low birth weight infants amounts to conditioning on that variable.
- Using our knowledge of (in)dependence relations in DAGs, explain this quote about Figure 3.1 from the paper: “Under this scenario, the crude mortality rate ratio for smoking would be greater than 1, whereas the adjusted rate ratio and, equivalently, the stratum-specific rate ratios should be 1.”
- Explain why Figure 3.2 implies that the crude and adjusted mortality rate ratios would be the same.
- In Figure 3.5, the authors do not include an arrow from Smoking to Mortality, but they use this diagram to explain how the birth weight paradox could arise. Why is excluding this arrow a key part of their argumentation?
- Using Figure 3.5, explain how the paradox arises by using the ideas of d-separation.
- Figure 3.7 is the most realistic of the causal diagrams. Explain how the paradox arises in this setting.
- In Figure 3.7, would the paradox have arisen if LBW-Type A had been the selection criterion instead of LBW? Would the paradox have arisen if LBW-Type B had been the selection criterion?
- Let’s generalize the key findings in this paper. The term selection bias broadly describes bias in results due to the way in which study participants are selected. How did selection bias come about for the birth weight paradox? Can we generalize this occurrence in terms of more general graph properties?