Topic 7 Graphical Structure of Selection Bias
Learning Goals
- Apply d-separation to block noncausal paths in causal DAGs with and without unobserved variables
- Differentiate confounding and selection bias in terms of graph structure and how they arise in applied studies
Slides from today are available here.
Exercises
Exercise 1
First, think through the relationships depicted in the causal graphs below and whether they make sense. These are intended to reflect a range of scenarios for why people drop out of studies.
Then for each of the graphs, identify the set of variables needed to achieve conditional exchangeability of the treatment \(A\) and outcome \(Y\). (\(U\) and \(W\) are unmeasured.) Check your answers to one of the graphs using DAGitty.
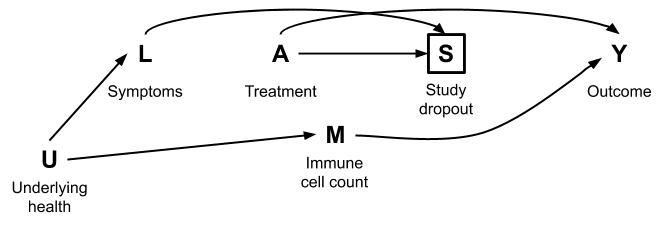
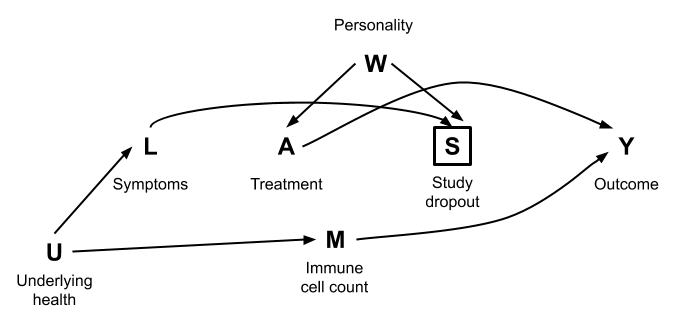
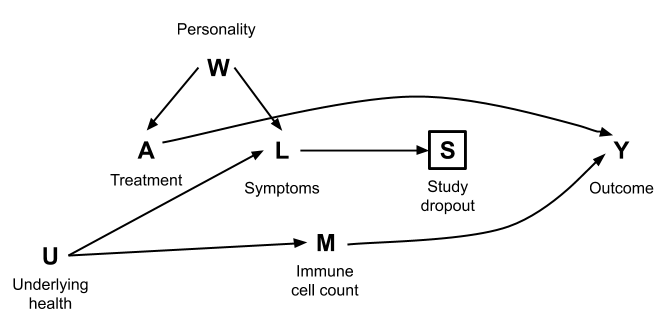
Exercise 2
In this exercise, we’ll consider how causal graphs can inform study design. (Inspired by a 1970s study on the relationship between estrogen use and endometrial cancer.)
Researchers have noticed a consistent association between use of a certain drug and disease. Research groups debated two hypotheses:
- The drug does cause disease.
- The drug doesn’t actually cause disease but leads to a side effect, leading to more frequent doctor visits, leading to increased diagnosis of existing disease.
The following study plan was proposed: restrict the study only to those with side effects and compare disease rates in drug-users and non-users. In this way, all participants have the same chance of being diagnosed.
The following causal graphs correspond to the two hypotheses:
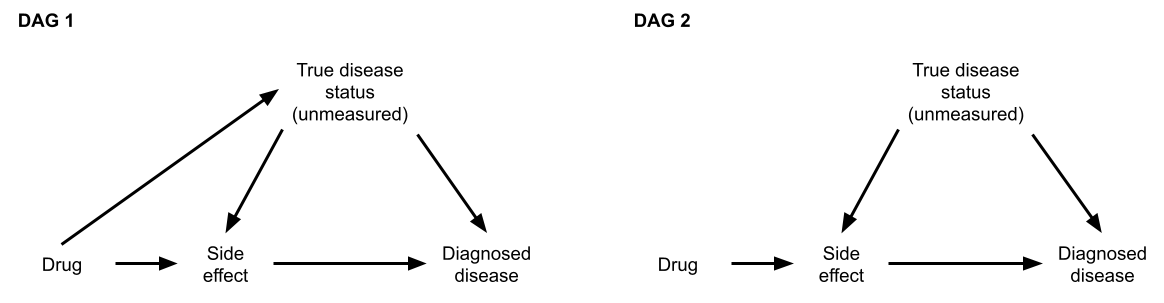
(The graphs don’t show confounders of the drug-true disease relationship for compactness. We can assume that these have already been adjusted for.)
Study design 1
Consider the study proposal above: restrict analysis to those with side effects.
Before looking at the causal graphs: does the rationale for this study design make sense? Why did researchers want to only look at patients with side effects?
Under this study design, the researchers were expecting that if Hypothesis 1 were correct (the drug does cause disease), they would find an association between drug use and diagnosed disease. They expected that if Hypothesis 2 were correct (the drug does NOT cause disease), they would find NO association between drug use and diagnosed disease.
- Are these expectations correct? Explain in light of the causal graphs.
Based on your answer above, is this an effective study design for the research questions of interest? That is, can this study proposal distinguish between the two hypotheses?
Study design 2
Consider another study proposal: ensure that everyone is screened for disease frequently, and we don’t restrict our analysis to only those with side effects.
What arrow can be removed as a result of this study design? (It might help to draw an updated version of DAGs 1 and 2 with this arrow removed.)
Under this study design, the researchers had the same expectations: if Hypothesis 1 were correct, they would find an association between drug use and diagnosed disease. If Hypothesis 2 were correct, they would find NO association between drug use and diagnosed disease.
- Are these expectations correct? Explain in light of the causal graphs.
Based on your answer above, is this an effective study design for the research questions of interest? That is, can this study proposal distinguish between the two hypotheses?
Exercise 3
In 2020, a COVID-19 risk factory study received a lot of press for the surprising finding that smoking seemed protective for COVID-19 mortality.
Dr. Eleanor Murray posted a series of Tweets diving into the situation from a causal graphs perspective. Read through her Tweets and discuss the following:
- How might we explain the paradoxical protective effect of smoking found in the risk factor study?
- Dr. Murray also discusses the importance of clarifying a causal question and the “Table 2 Fallacy.” Did any of these other ideas resonate with you, pique your curiosity, or leave you uncertain?
- Comment on the structure of the Tweetorial. What was effective and less effective? Would you have presented the information differently? Using different causal graphs? (If you feel inclined, put your ideas in Tweet form!)