Topic 16 Graphical Structure of Mediation

Pre-class work

Videos/slides

Checkpoint





Learning Goals

  • Relate d-separation ideas to exchangeability conditions for mediation
  • MEDI1: Formulate research questions that can be answered via mediation analysis





Exercises

Solutions to these exercises are available on Moodle.

Background

Consider the following causal diagram representing variables important in mediation analysis:

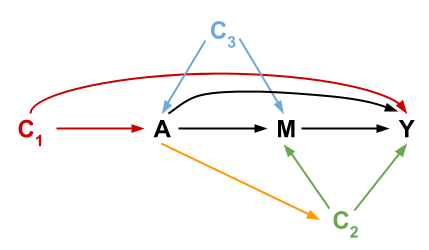
Let \(C = \{C_1, C_2, C_3\}\). When trying to estimate mediation effects (CDE, NDEs, NIEs), the following 4 exchangeability assumptions are necessary:

  1. \(Y^{am} \perp\!\!\!\perp A \mid C\)
  2. \(Y^{am} \perp\!\!\!\perp M \mid A, C\)
  3. \(M^{a} \perp\!\!\!\perp A \mid C\)
  4. \(Y^{am} \perp\!\!\!\perp M^{a*} \mid C\)


These 4 exchangeability assumptions can be expressed as the following 4 graphical assumptions:

  1. No unmeasured confounders of the treatment-outcome relationship (\(A\) and \(Y\)).
  2. No unmeasured confounders of the mediator-outcome relationship (\(M\) and \(Y\)).
  3. No unmeasured confounders of the treatment-mediator relationship (\(A\) and \(M\)).
  4. No confounder of the mediator-outcome relationship is affected by treatment (arrows from \(A\) to \(C_2\)).

When these 4 assumptions hold, the CDE, NDEs, and NIEs can be estimated from data, and we can use models such as the regression models below to estimate them. (\(C = \{C_1, C_2, C_3\}\))

\[ E[Y\mid A, M, C] = \theta_0 + \theta_1 A + \theta_2 M + \theta_3 AM + \mathbf{\theta_4'C} \] \[ E[M\mid A, C] = \beta_0 + \beta_1 A + \mathbf{\beta_2'C} \]



Exercise 1

Assumptions 1 and 2 are needed in order to estimate the controlled direct effect (CDE).

Using d-separation ideas, argue why Assumptions 1 and 2 must hold but why it is not necessary for Assumptions 3 and 4 to hold. Use the paths below from \(A\) to \(Y\) in your arguments.

(Note: All 4 assumptions must hold to estimate the natural direct and indirect effects. If you finish early, feel free to tackle exploring this graphically by looking at the \(M\) to \(Y\) and \(A\) to \(M\) paths below.)

## Path 1:   A <- C1 -> Y  
## Path 2:   A -> Y  
## Path 3:   A <- C3 -> M -> Y  
## Path 4:   A <- C3 -> M <- C2 -> Y  
## Path 5:   A -> M -> Y  
## Path 6:   A -> M <- C2 -> Y  
## Path 7:   A -> C2 -> Y  
## Path 8:   A -> C2 -> M -> Y
## Path 1:   A <- C1 -> Y <- M  
## Path 2:   A <- C1 -> Y <- C2 -> M  
## Path 3:   A -> Y <- M  
## Path 4:   A -> Y <- C2 -> M  
## Path 5:   A <- C3 -> M  
## Path 6:   A -> M  
## Path 7:   A -> C2 -> Y <- M  
## Path 8:   A -> C2 -> M
## Path 1:   M <- A <- C1 -> Y  
## Path 2:   M <- A -> Y  
## Path 3:   M <- A -> C2 -> Y  
## Path 4:   M -> Y  
## Path 5:   M <- C3 -> A <- C1 -> Y  
## Path 6:   M <- C3 -> A -> Y  
## Path 7:   M <- C3 -> A -> C2 -> Y  
## Path 8:   M <- C2 <- A <- C1 -> Y  
## Path 9:   M <- C2 <- A -> Y  
## Path 10:   M <- C2 -> Y



Exercise 2

Under the exchangeability assumptions discussed above, we can use models such as the regression models below to estimate the CDE, NDE, and NIE. (\(C = \{C_1, C_2, C_3\}\), and \(\theta_4, \beta_2\) are vectors of coefficients.) In particular, these models can be used as structural models to simulate the different potential outcomes needed to estimate these effects.

\[ E[Y\mid A, M, C] = \theta_0 + \theta_1 A + \theta_2 M + \theta_3 AM + \theta_4'C \] \[ E[M\mid A, C] = \beta_0 + \beta_1 A + \beta_2'C \]

Given these models, derive expressions for \(CDE(m)\) and \(NDE(0)\).



Exercise 3

Suppose that we were interested in the effect of a new funding model for police departments on crime rates. What causal questions related to mediation might arise? What effects might be most of interest and why?