Topic 10 Logistic Regression

10.1 Discussion

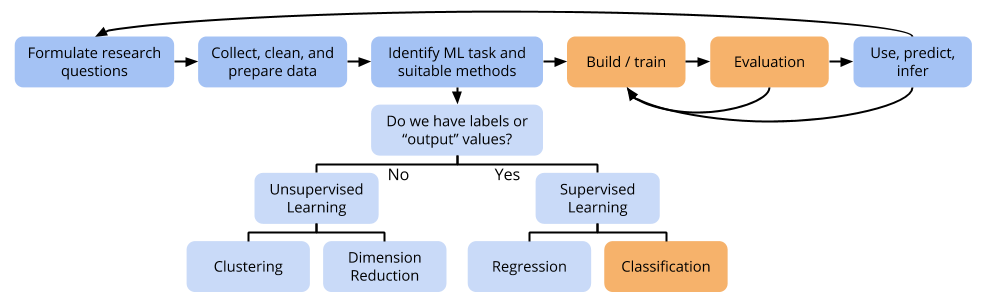
Linear vs Logistic Regression

Linear regression assumptions
$y$ is a quantitative response variable with
\[y = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p + \varepsilon \qquad \text{ where } \qquad \varepsilon \stackrel{ind}{\sim} N(0, \sigma^2)\]
Logistic regression assumptions
$y$ is a binary (0/1) response variable.
Let $P(y=1 \mid x)$ denote the probability that $y=1$ given (as a function of) values of the predictors $x$.
A Bernoulli model is a model for binary responses (a coin flip model). Then
\[y \stackrel{ind}{\sim} \text{Bernoulli}(P(y=1 \mid x)) \qquad \text{ i.e. } y = \begin{cases} 1 & \text{ w/ probability } P(y=1 \mid x) \\ 0 & \text{ w/ probability } 1-P(y=1 \mid x) \\ \end{cases}\] where \[\log \left(\frac{P(y=1 \mid x)}{1-P(y=1 \mid x)} \right) = \log \left(\text{odds}(y=1 \mid x) \right) = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p\] equivalently \[P(y=1 \mid x) = \frac{e^{\beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p}}{1 + e^{\beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p}}\]
Note: in statistics, “log” is the natural log (ln) by default
- If we wish to use logistic regression for statistical inference:
  - There are link tests to test whether $\log(p/(1-p))$ is a good function to use on the left to link to the predictors.
  - There is a test for checking whether the linear terms on the right suffice (Box-Tidwell test).
- We will focus on using logistic regression for prediction purposes.

Using a logistic regression model for prediction

Given values of predictor variables, the log odds is given directly.
Transform to odds by exponentiating
Transform to probability with $p = \text{odds}/(1+\text{odds})$
Applying a probability threshold gives hard classifications
- Overall accuracy: out of all cases, fraction of correct classifications
- Sensitivity: out of the cases that are truly positive, how many of those were correctly classified as positive?
- Specificity: out of the cases that are truly negative, how many of those were correctly classified as negative?
Why look at just one probability threshold?
- We will look at many thresholds.
- We’ll explore a new computing tool in R, for loops, to loop over many thresholds.
- Through this, we’ll build up another evaluation tool: the ROC curve (receiver operating characteristic) and also AUC (area under the ROC curve).

10.2 Exercises

You can download a template RMarkdown file to start from here.

Machine learning models provide a powerful tool for medical diagnosis. In these exercises, we’ll look at data collected by Dr. Henrique da Mota available on the UCI Machine Learning Repository. We’ll use this data to develop models that can be used to diagnose orthopedic patients’ vertebral columns as “irregular” or “regular”. Irregular vertebral columns either exhibit spondilolysthesis (a condition where one vertebra is displaced relative to another) or disk hernia (a condition in which connective tissue between vertebra is damaged).

For each of 309 patients, the dataset contains 6 vertebral measurements (potential predictors) along with the patient’s vertebral class (1 = irregular, 0 = regular). It’s important to keep in mind that each row in the dataset represents a real patient:

library(dplyr)
vert <- read.csv("https://www.macalester.edu/~ajohns24/data/vertebral_column.csv")

# Remove an outlier and make the "class" column categorical
vert <- vert %>% 
    filter(spondylolisthesis_grade < 300) %>%
    mutate(class = as.factor(class))

# Check out the first few rows
head(vert, 3)

##   pelvic_incidence pelvic_tilt lumbar_angle sacral_slope pelvic_radius
## 1            63.03       22.55        39.61        40.48         98.67
## 2            39.06       10.06        25.02        29.00        114.41
## 3            68.83       22.22        50.09        46.61        105.99
##   spondylolisthesis_grade class
## 1                   -0.25     1
## 2                    4.56     1
## 3                   -3.53     1

# How many patients of each class are there?
table(vert$class)

## 
##   0   1 
## 100 209

Thinking about assumptions
Suppose that we used hypothesis tests to assess logistic regression assumptions and determined that assumptions could be violated. What would be the implications for statistical inference? Specifically what could you say about the performance of 99% confidence intervals?

Planning model evaluation
You’ll be comparing a few models for predicting vertebral class. Describe how cross-validation can be used to fairly compare models. Outline the procedure and how a final metric is computed.

Fitting logistic regression in caret
We’ll explore a logistic regression model with all predictors. You can fit this model in caret as below.
- method = "glm" means “generalized linear model” (GLM). Logistic regression is a linear model (the right hand side). The “generalized” indicates that more types of response variables than just quantitative (for linear regression) can be considered.
- family = binomial: The Bernoulli model is a model for one trial (one coin flip). The binomial model is a model for multiple trials (multiple coin flips). This is how you communicate that you want logistic regression as opposed to some other GLM.
- metric = "Accuracy": as opposed to “RMSE” in the regression setting
- trControl: Fill this in to use 10-fold CV.
```
set.seed(333)
vert_mod <- train(
    class ~ .,
    data = vert,
    method = "glm",
    family = binomial,
    metric = "Accuracy",
    trControl = trainControl(???),
    na.action = na.omit
)
```

Nailing down caret’s evaluation metrics
1. When you print vert_mod or vert_mod$results, the CV-estimated accuracy is reported. Verify this estimate by hand by using the Accuracy column within vert_mod$resample. (To access a column, use $column_name.)
2. caret has a confusionMatrix() function that takes as input predictions from a model and the true classes. It outputs the confusion matrix and a number of accuracy metrics and statistics. We also specify which of “0” or “1” is the “positive” class.
  There are a lot of metrics computed and reported! We are not going to focus on all of them, but we will try to make sense of many. You’ll check many of these by hand using the confusion matrix at the top. (Don’t worry about Kappa or McNemar for now.)
```
# predict() below uses 0.5 as a probability threshold by default
mod_pred <- predict(vert_mod, newdata = vert)
# Compute confusion matrix and statistics
conf_mat <- confusionMatrix(data = mod_pred, reference = vert$class, positive = "1")
# Print results
conf_mat
```
3. Compute by hand the overall accuracy and check against “Accuracy”.
  - The “95% CI” is a 95% confidence interval for that Accuracy estimate. What information does it give us?
4. What in the world is “No Information Rate” (NIR)? It’s something quite useful actually. Consider the most simplistic classfier in which we always predict the majority class for all cases. What class makes up the majority of the cases? Verify by hand that the fraction of cases in this majority class is the “No Information Rate”.
  - The p-value beneath corresponds to testing the null hypothesis that Accuracy=NIR versus the alternative that Accuracy > NIR. What information does the p-value give us?
5. Compute sensitivity and specificity by hand and check against the output.
6. Positive and negative predictive value “flip” the probability statements of sensitivity and specificity. That is, sensitivity is the probability of classifying a case as positive GIVEN that they are truly positive ($P(\text{classify positive} \mid \text{truly positive})$ in probability notation). Positive predictive value (PPV) flips this to being the probability of a case truly being positive GIVEN that they were predicted to be positive ($P(\text{truly positive} \mid \text{classify positive})$ in probability notation).
  Why are PPV and NPV useful in practice? If you were a spinal physician, would you use this model in the clinic?

Note: If you want to learn more about the metrics that caret outputs, read the documentation by entering ?caret::confusionMatrix in the Console.

Varying the probability threshold: for-loops
Here, you’ll explore how to write a for-loop to evaluate a logistic regression model at many probability thresholds.
Step through the code and comments (comments start with a # pound sign) to understand some general features about looping operations in R. If you ever want to look up the documentation for a function, you can enter ?function_name in the Console.
Also fill in the ???’s in the code.

# Obtain the actual observed vertebral classes from the data
actual_classes <- vert$class
# Obtain the predicted probability of vertebral irregularity (Y=1 event)
# type="response" converts log odds, to odds, and finally to a probability
pred_probs <- predict(vert_mod$finalModel, newdata = vert, type = "response")

# Create a regularly-spaced sequence of probability thresholds
prob_threshs <- seq(0, 1, by = 0.01)

# Create empty vectors to store the sensitivity and specificity
# for all values of the probability thresholds
sens_vec <- rep(0, length(prob_threshs))
spec_vec <- rep(0, length(prob_threshs))

# Loop over all of the thresholds
# seq_along() makes a sequence 1,2,...,length of prob_threshs
# In each iteration of the loop, the variable i takes these integer values
for (i in seq_along(prob_threshs)) {
    # Get the probability threshold for this iteration
    thresh <- prob_threshs[i]
    # If the predicted prob > threshold, predict "1".
    # Otherwise, predict "0".
    hard_preds <- ifelse(pred_probs > thresh, "1", "0")
    # Create boolean TRUE/FALSE vectors indicating whether the
    # prediction for each case is a TP, TN, FP, FN.
    is_tp <- hard_preds=="1" & actual_classes=="1"
    is_tn <- ???
    is_fp <- ???
    is_fn <- ???
    # Calculate sensitivity and specificity
    # Hint: sum(is_tp) gives the number of TPs
    sensitivity <- ???
    specificity <- ???
    # Store sensitivity specificity in their containers
    sens_vec[i] <- sensitivity
    ???
}

ROC curves and AUC
1. An ROC curve plots sensitivity on the y-axis versus 1-specificity on the x-axis. In this way, the y=x line provides a convenient reference for a random guessing classifier (flips a coin to make the classification).
```
plot(1-spec_vec, sens_vec)
abline(a = 0, b = 1, col = "gray")
```
2. What would the ROC curve look like for a model that is uniformly better for every probability threshold? For a model that is uniformly worse for each threshold?
3. What if ROC curves cross each other? A convenient way to quantify differences between models is with the area under the ROC curve, called AUC. The code below shows how you would compute AUC by hand.
```
roc_fun <- approxfun(x = 1-spec_vec, y = sens_vec)
integrate(roc_fun, lower = 0, upper = 1)
```
  What is the AUC for a perfect classifier? For the random guessing classifier?

You might imagine that there is an R package for making ROC curves and calculating AUC. There is! You will explore the pROC package in your homework.