Topic 1 Motivation and Review

1.1 Activity: motivating main ideas

In each of the following situations, there is some behind-the-scenes code that performs an analysis and generates some output plots. Brainstorm what research question(s) are trying to be answered in each of the situations by looking at the first few rows of data and the plots.

Situation A

We have 10,000 observations on the following variables:

  • ID: Identification
  • Income: Income in $10,000’s
  • Limit: Credit limit
  • Rating: Credit rating
  • Cards: Number of credit cards
  • Age: Age in years
  • Education: Number of years of education
  • Gender: A factor with levels Male and Female
  • Student: A factor with levels No and Yes indicating whether the individual was a student
  • Married: A factor with levels No and Yes indicating whether the individual was married
  • Ethnicity: A factor with levels African American, Asian, and Caucasian indicating the individual’s ethnicity
  • Balance: Average credit card balance in $.
## Look at the first few rows
head(Credit)
##   ID  Income Limit Rating Cards Age Education Gender Student Married
## 1  1  14.891  3606    283     2  34        11   Male      No     Yes
## 2  2 106.025  6645    483     3  82        15 Female     Yes     Yes
## 3  3 104.593  7075    514     4  71        11   Male      No      No
## 4  4 148.924  9504    681     3  36        11 Female      No      No
## 5  5  55.882  4897    357     2  68        16   Male      No     Yes
## 6  6  80.180  8047    569     4  77        10   Male      No      No
##   Ethnicity Balance
## 1 Caucasian     333
## 2     Asian     903
## 3     Asian     580
## 4     Asian     964
## 5 Caucasian     331
## 6 Caucasian    1151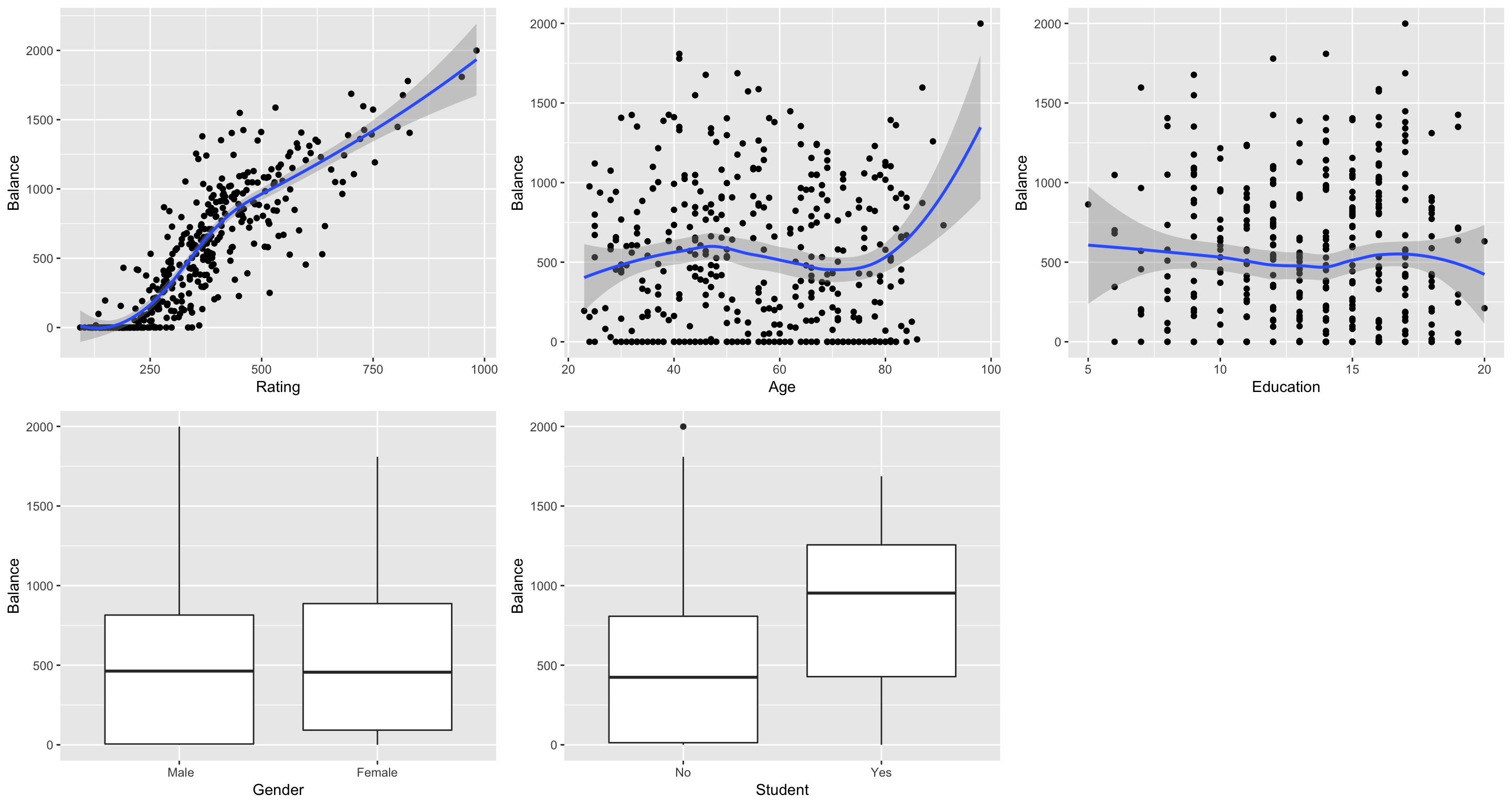

Situation B

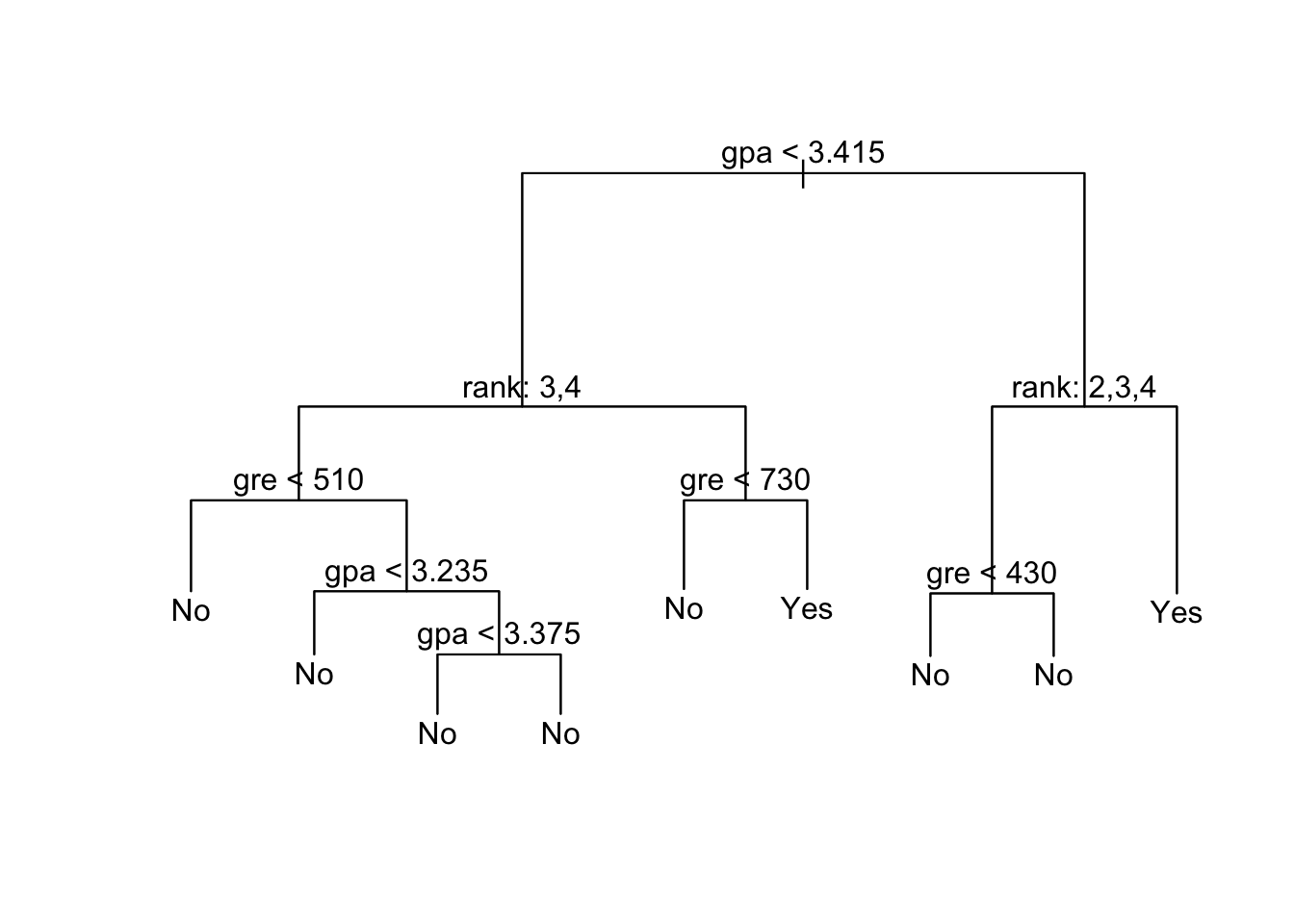
We have 400 observations of the following variables:

  • admit: binary variable; 0 = rejected, 1 = admitted
  • gre: applicant’s GRE score
  • GPA: applicant’s undergraduate GPA
  • rank: A “prestige” ranking of the applicant’s undergraduate institution. 1 to 4 going from least to most prestigious
head(grad)
##   admit gre  gpa rank
## 1    No 380 3.61    3
## 2   Yes 660 3.67    3
## 3   Yes 800 4.00    1
## 4   Yes 640 3.19    4
## 5    No 520 2.93    4
## 6   Yes 760 3.00    2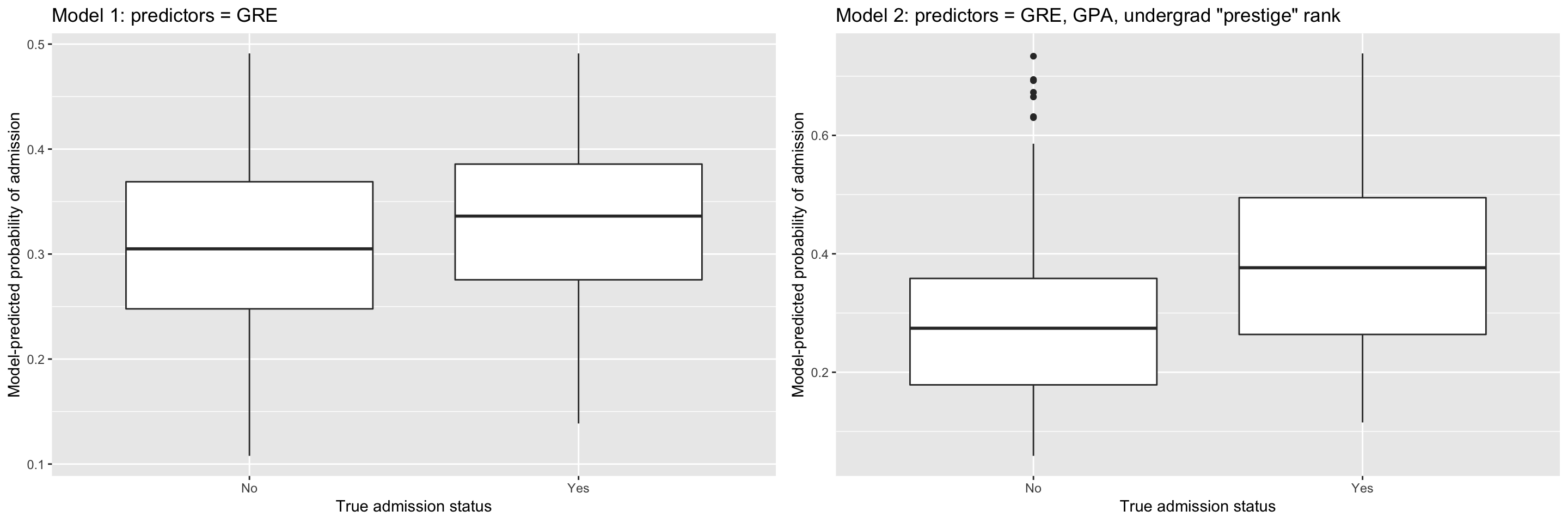

Situation C

We have 85 different Halloween candies and measured the following variables:

  • competitorname: The name of the Halloween candy.
  • chocolate: Does it contain chocolate?
  • fruity: Is it fruit flavored?
  • caramel: Is there caramel in the candy?
  • peanutyalmondy: Does it contain peanuts, peanut butter or almonds?
  • nougat: Does it contain nougat?
  • crispedricewafer: Does it contain crisped rice, wafers, or a cookie component?
  • hard: Is it a hard candy?
  • bar: Is it a candy bar?
  • pluribus: Is it one of many candies in a bag or box?
  • sugarpercent: The percentile of sugar it falls under within the dataset.
  • pricepercent: The unit price percentile compared to the rest of the dataset.
  • winpercent: The overall win percentage according to 269,000 matchups.
head(candy_rankings)
##   competitorname chocolate fruity caramel peanutyalmondy nougat
## 1      100 Grand      TRUE  FALSE    TRUE          FALSE  FALSE
## 2   3 Musketeers      TRUE  FALSE   FALSE          FALSE   TRUE
## 3       One dime     FALSE  FALSE   FALSE          FALSE  FALSE
## 4    One quarter     FALSE  FALSE   FALSE          FALSE  FALSE
## 5      Air Heads     FALSE   TRUE   FALSE          FALSE  FALSE
## 6     Almond Joy      TRUE  FALSE   FALSE           TRUE  FALSE
##   crispedricewafer  hard   bar pluribus sugarpercent pricepercent
## 1             TRUE FALSE  TRUE    FALSE        0.732        0.860
## 2            FALSE FALSE  TRUE    FALSE        0.604        0.511
## 3            FALSE FALSE FALSE    FALSE        0.011        0.116
## 4            FALSE FALSE FALSE    FALSE        0.011        0.511
## 5            FALSE FALSE FALSE    FALSE        0.906        0.511
## 6            FALSE FALSE  TRUE    FALSE        0.465        0.767
##   winpercent
## 1   66.97173
## 2   67.60294
## 3   32.26109
## 4   46.11650
## 5   52.34146
## 6   50.34755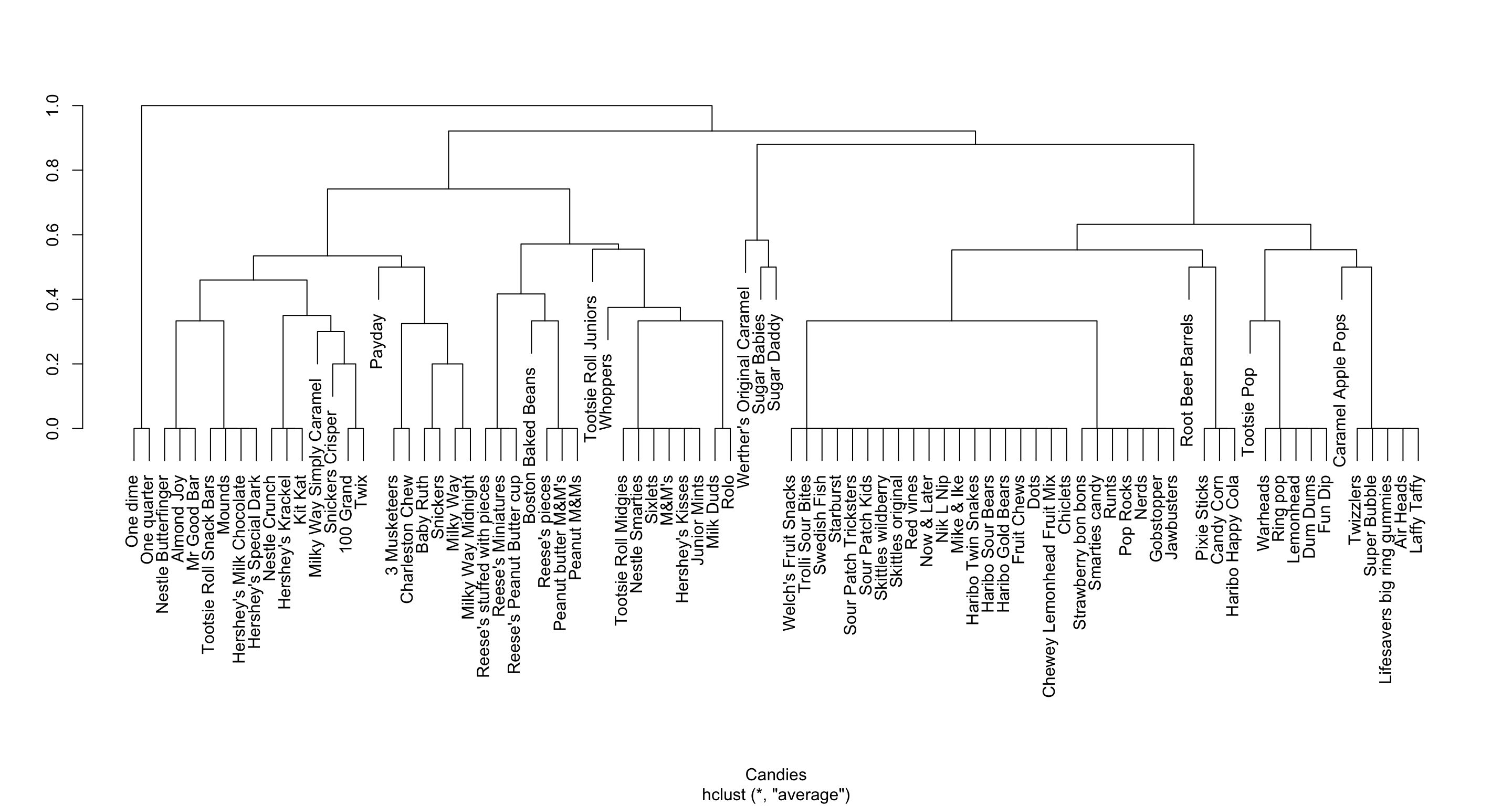

1.2 Review exercises

The following exercises are meant to help you remember key concepts from Math 155 and help you get used to working with R again. All code is provided, but make sure that you understand the general structure so that you could write your own code in the future, with the aid of a reference sheet. (Suggestion: Make a code reference sheet for yourself!)

So that you don’t have to copy and paste the code, download and work from the template file here. This is an RMarkdown file that you can open in RStudio. You won’t need to write new code, but you may find it helpful to add notes and comments. (Note: When you go to save this file to your computer, your browser may append a “.txt” to the end of the filename. Delete this extra file extension, and select “All Files” from the “Format” dropdown menu at the bottom of the Save As box.)


You will submit your answers to these questions for Homework 1 (on Moodle).



Data context: We have data on over a thousand homes in upstate New York. This data contains information on house price as well as several other physical characteristics of the house.

library(ggplot2)
library(dplyr)
homes <- read.delim("http://sites.williams.edu/rdeveaux/files/2014/09/Saratoga.txt")

Before getting started on the exercises, take a minute to familiarize yourself with the data structure:

# Look at the first 6 rows. What are the cases? What are the variables?
head(homes)

# Obtain the dimensions of the data. How many cases? How many variables?
dim(homes)

# Look at just the variable names
colnames(homes)

  1. Visualizing the response variable
    Construct a visualization of house price:

    # Histogram
ggplot(homes, aes(x = Price)) + 
    geom_histogram()

# Density plot
ggplot(homes, aes(x = Price)) +
    geom_density()
    Question: How would you describe the shape of the distribution?
    1. Left-skewed
    2. Right-skewed



  1. A simple linear regression model
    We want to explore the relationship between house price and square footage (Living.Area variable):

    Price = \(f\)(Living.Area) + \(\varepsilon\) = \(\beta_0\) + \(\beta_1\)Living.Area + \(\varepsilon\)

    We can visualize the relationship with a scatterplot with an overlaid estimated linear trend line (geom_smooth(method = "lm")):

    ggplot(homes, aes(x = Living.Area, y = Price)) + 
    geom_point() +
    geom_smooth(method = "lm")

    In R we can obtain an equation for the model line above. This equation is an estimate for the population model:

    Price = \(\hat{f}\)(Living.Area) + \(\varepsilon\) = \(\hat\beta_0\) + \(\hat\beta_1\)Living.Area + \(\varepsilon\) 
    # Fit the model
mod1 <- lm(Price ~ Living.Area, data = homes)

# Print the summarized output from the model
summary(mod1)
    Question: Which of the following is the correct estimated model formula?
    1. Price = 113.123 + 13439.394 Living.Area + \(\varepsilon\)
    2. Price = 13439.394 + 113.123 Living.Area + \(\varepsilon\)



  1. Predictions
    Consider a house that has a square footage of 1000 square feet. Use mod1 to predict the price of this house. (Round to the nearest dollar.)



  1. Residuals
    A particular house in the dataset has a square footage of 1000 and was priced at $100,000. Using your prediction from the previous exercise (rounded to the nearest dollar), calculate the residual (true value - predicted value) for this house.



  1. Adding a categorical variable
    In addition to Living.Area let’s consider the Fuel.Type variable which has 3 categories: fuel types 2, 3, or 4. We can visualize how fuel type relates to house price with these plots:

    # Adding fuel as a color to the existing scatterplot
ggplot(homes, aes(x = Living.Area, y = Price, color = factor(Fuel.Type))) + 
    geom_point(alpha = 0.2) +
    geom_smooth(method = "lm")

# Visualizing price and fuel alone
ggplot(homes, aes(x = factor(Fuel.Type), y = Price)) + geom_boxplot()
    We can model this with the multiple linear regression model (“multiple” = multiple predictor variables):
    Price = \(f\)(Living.Area, Fuel.Type) + \(\varepsilon\)
    Price = \(\beta_0\) + \(\beta_1\)Living.Area + \(\beta_2\)Fuel.Type2 + \(\beta_3\)Fuel.Type3 + \(\varepsilon\)

    Note that Fuel.Type2 and Fuel.Type3 are indicator variables where, for example, Fuel.Type2 equals 1 if the house uses fuel type 2 and 0 otherwise. To fit this model in R:

    mod2 <- lm(Price ~ Living.Area + factor(Fuel.Type), data = homes)
summary(mod2)

    (Note: enclosing Fuel.Type within factor() forces R to treat it as a categorical variable. By default, Fuel.Type consists of the integers 2, 3, and 4.)
    Question: Using this model, what price would you predict for a house that uses fuel type 2 and has a square footage of 1000? (Round to the nearest dollar.)



  1. Interpreting coefficients in a multivariate model
    What is the interpretation of the factor(Fuel.Type)3 coefficient in mod2?
    1. The average price for a house that uses fuel type 3.
    2. The average price for a house that uses fuel type 3, holding constant square footage.
    3. The difference in average price for a house that uses fuel type 3 compared to a house that uses fuel type 2
    4. The difference in average price for a house that uses fuel type 3 compared to a house that uses fuel type 2, holding constant square footage.



  1. Interpreting coefficients in a multivariate model
    What is the interpretation of the Living.Area coefficient in mod2?
    1. The average increase in price for each extra square foot
    2. The average increase in price for each extra square foot, holding constant fuel type
    3. The average increase in price for each extra square foot, only for houses that use fuel type 2
    4. The average increase in price for each extra square foot, only for houses that use fuel type 3
    5. The average increase in price for each extra square foot, only for houses that use fuel type 4



  1. Statistical inference: confidence intervals
    In mod2 we see that the estimate of \(\beta_1\) is \(\hat\beta_1 = 110.231\) and has a standard error of \(SE(\hat\beta_1) = 2.784\). Which of the following provides an approximate 95% confidence interval for \(\beta_1\)?
    1. \(110.231 \pm 2.784 = (107.447, 113.015)\)
    2. \(110.231 \pm 2\times 2.784 = (104.663, 115.799)\)
    3. \(110.231 \pm 3\times 2.784 = (101.879, 118.583)\)



  1. Confidence interval interpretation
    How can we interpret the 95% confidence interval?
    1. There’s a 95% chance that \(\beta_1\) is in this interval.
    2. There’s a 95% chance that our sample would produce a 95% confidence interval that covers \(\beta_1\).



  1. Confidence interval interpretation
    Notice that 0 is not in the 95% confidence interval for \(\beta_1\). What does this tell us?
    1. We have significant evidence that house price increases as square footage increases, holding constant fuel type.
    2. We do not have significant evidence that house price increases as square footage increases, holding constant fuel type.



  1. Statistical inference: p-values
    The p-value in the Living.Area row corresponds to the test that:
    \(H_0: \beta_1 = 0\)
    \(H_a: \beta_1 \neq 0\)
    What can we conclude from the p-value?
    1. We have significant evidence that house price increases as square footage increases, holding constant fuel type.
    2. We do not have significant evidence that house price increases as square footage increases, holding constant fuel type.



  1. Interpreting p-values
    How can we interpret the p-value?
    1. There’s a tiny chance that there’s no relationship between house price and square footage holding constant fuel type (\(\beta_1=0\)).
    2. There’s a tiny chance that there’s any relationship between house price and square footage holding constant fuel type (\(\beta_1 \neq 0\)).
    3. If in fact only there were no relationship between house price and square footage holding constant fuel type, there’s a tiny chance we’d have gotten this sample of data in which there were such a strong positive relationship.



  1. Thinking about fireplaces
    Let’s think about both square footage (Living.Area) and about whether or not a house has any fireplaces. Below, we create a binary variable called AnyFireplaces that is TRUE if the number of fireplaces is greater than 0 and that is FALSE otherwise.

    homes <- homes %>%
    mutate(AnyFireplaces = Fireplaces > 0)

    We can visualize both of these predictors as follows:

    ggplot(homes, aes(x = Living.Area, y = Price, color = AnyFireplaces)) + 
    geom_point(alpha = 0.2) +
    geom_smooth(method = "lm")

    Consider two models that use AnyFireplaces:

    mod3 <- lm(Price ~ Living.Area + AnyFireplaces, data = homes)
summary(mod3)
mod4 <- lm(Price ~ Living.Area * AnyFireplaces, data = homes)
summary(mod4)
    Question: Consider the research question: “Is a square foot worth the same amount in a home with a fireplace as in a home without a fireplace?” Which of mod3 and mod4 can answer this question?
    1. mod3
    2. mod4



  1. Consider the research question: “How much is a square foot worth, holding fixed whether or not a house has a fireplace?” Which of mod3 and mod4 can answer this question?
    1. mod3
    2. mod4



  1. Which of mod3 and mod4 would be called an interaction model?
    1. mod3
    2. mod4



  1. Summarizing interaction models
    Using the interaction model chosen in the previous exercise, which of the following represents the relationship between Price and Living.Area for homes without fireplaces?
    1. Price = (40901.294-37610.413) + 92.364 Living.Area
    2. Price = (40901.294-37610.413) + (92.364+26.852) Living.Area
    3. Price = 40901.294 + (92.364+26.852) Living.Area
    4. Price = 40901.294 + 92.364 Living.Area



  1. Summarizing interaction models
    Which of the following represents the relationship between Price and Living.Area for homes with fireplaces?
    1. Price = (40901.294-37610.413) + 92.364 Living.Area
    2. Price = (40901.294-37610.413) + (92.364+26.852) Living.Area
    3. Price = 40901.294 + (92.364+26.852) Living.Area
    4. Price = 40901.294 + 92.364 Living.Area



  1. Inference in interaction models
    At a significance level of 0.01, what can we conclude about the relationship between price and square footage in homes without fireplaces and in homes with fireplaces in the general population?
    1. A square foot in a home with a fireplace is worth more than a square foot in a home without a fireplace.
    2. We don’t have evidence to say that a square foot in a home with a fireplace is worth more than a square foot in a home without a fireplace.



  1. Inference in interaction models
    What could we say about the 99% confidence interval for the interaction coefficient?
    1. It lies completely above 0.
    2. It lies completely below 0.
    3. It contains 0.