Topic 5 Subset Selection

5.1 Discussion

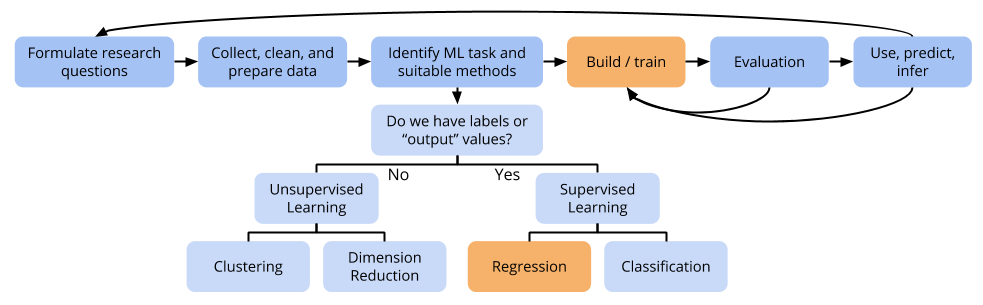
Subset selection methods

Automated methods that take different strategies for exploring subsets of the predictors
Stepwise selection methods: add or remove variables one at a time
Best subset selection: brute force method that tries all possible subsets of predictors

5.2 Exercises

You can download a template RMarkdown file to start from here.

We’ll continue using the body fat dataset to explore subset selection methods.

library(ggplot2)
library(dplyr)
bodyfat <- read.csv("http://www.macalester.edu/~ajohns24/data/bodyfatsub.csv")

# Take out the redundant Density and HeightFt variables
bodyfat <- bodyfat %>% 
    select(-Density, -HeightFt)

Backward stepwise selection: by hand
In the backward stepwise procedure, we start with the full model, full_model, with all predictors:
```
full_model <- lm(BodyFat ~ Age + Weight + Height + Neck + Chest + Abdomen + Hip + Thigh + Knee + Ankle + Biceps + Forearm + Wrist, data = bodyfat)
```
Then…
- Identify which predictor contributes the least to the model. One approach is to identify the least significant predictor.
- Fit a new model which eliminates this predictor.
- Identify the least significant predictor in this model.
- Fit a new model which eliminates this predictor.
- Repeat 1 more time to get the hang of it.

Interpreting the results
1. Examine which predictors remain after the previous exercise. Are you surprised that, for example, Wrist is still in the model but Weight is not? Does this mean that Wrist is a better predictor of body fat percentage than Weight is?
2. Forward selection is another stepwise technique. Can you guess how this differs from backward selection?
3. Best subset selection is another subset selection technique that looks at every possible subset of predictors, fits all of these models, and picks the best one. From the perspective of computational time, why is this not a preferable approach?

Planning backward selection using CV
Using p-values to perform backward selection by hand is convenient but not the most direct way to target predictive accuracy. Outline the steps that you would take to use cross-validation to perform backward selection. (Write an algorithm in words.)

Backward stepwise selection in caret
We can use the caret package to perform backward stepwise selection with cross-validation as shown below. (Note: CV is only used to pick among the best 1, 2, 3, …, and 13 variable models. To find the best 1, 2, 3, …, and 13 variable models, training MSE is used. caret uses training MSE because within a subset size, all models have the same number of coefficients, which makes both ordinary R-squared and training MSE ok.) Just focus on the structure of the code and how different parts of the output are used.
Is there a use case that you are interested in but don’t see below? Feel free to ask the instructor about it!
```
library(caret)

# Set up cross-validation information
train_ctrl_cv10 <- trainControl(method = "cv", number = 10)

# Perform backward stepwise selection
# The first time you run this, you'll be prompted to install the "leaps" package
set.seed(253)
back_step <- train(
    BodyFat ~ .,
    data = bodyfat,
    method = "leapBackward",
    tuneGrid = data.frame(nvmax = 1:13),
    trControl = train_ctrl_cv10,
    metric = "RMSE",
    na.action = na.omit
)

# Look at accuracy/error metrics for the different subset sizes
back_step$results

# What tuning parameter gave the best performance?
# i.e. What subset size gave the best model?
back_step$bestTune

# Obtain the coefficients for the best model
coefficients(back_step$finalModel, id = back_step$bestTune$nvmax)

# Use the best model to make predictions on new data
predict(back_step, newdata = bodyfat)
```
Some notes about the code:
- The BodyFat ~ . formula tells R that BodyFat is the response and that all predictors (specified with the .) will be considered.
- The tuneGrid argument allows us to input tuning parameters into the fitting process. The tuning parameters here are the number of variables included in the models (nvmax). This can vary from 1 to 13 (the maximum number of predictors possible).
- The metric argument indicates how the best of the 1-variable, 2-variable, etc. models will be chosen. We’ll use RMSE (root mean squared error).
- When you look at back_step$results, you’ll see a matrix of output. The rows correspond to the different subset sizes. For each subset size you’ll see the RMSE, $R^2$, and MAE accuracy/error metrics. Recall that these are estimates that arise by taking the mean of the values given in the 10 CV iterations. The 10 values from the 10 iterations also have a standard deviation. These are reported in the last 3 columns. What use might the standard deviation have in picking a final model?